Coordinate questions on the GRE will require you to infer from your knowledge of the coordinate plane, which is formed when two lines meet at right angles. One of the lines, the "up-and-down" line, is generally called the y axis, while the "left-and-right" line is called the x axis.

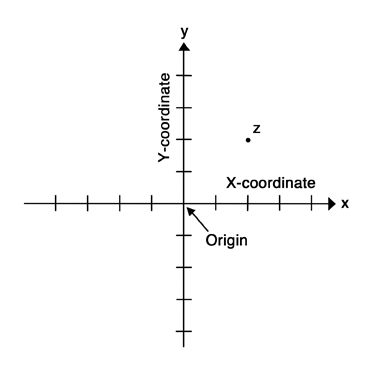
The coordinate plane is an easy way to designate unique points, as each point is given an x coordinate and y coordinate value. When reading from or determining the location of a point on the coordinate plane, note the following: Points to the right of the y axis have positive x values, while points to the left of the y axis have negative x values. Likewise, points above the x axis have positive y values, and points below the x axis have negative y values. In the coordinate-plane above, and assuming that each tick mark is one unit, point z has the coordinates (2,2), where the first number, 2, designates the x-coordinate, and 2 designates the y-coordinate.

Aside from a few "what is the coordinate of point P" or "what is the distance between points m and n" type of questions, there are not too many coordinate questions that have ever appeared on the GRE. Therefore, you'll need to be familiar with how to read a coordinate graph, how to calculate distance, and in rare instances, how to determine the slope of a line.

• Find the coordinate This is the easiest type of coordinate question, which requires you to simply read from the provided coordinate plane or infer a location from the information that you are given. For example, what is the coordinate of point z in each of the following coordinate planes?

  

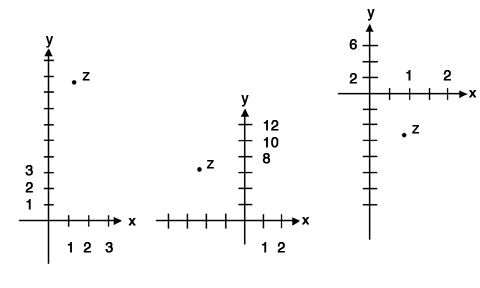
  In the graph on the left, the x coordinate of point z is a little bit more than 1, and the y coordinate of point z is almost 9, so a feasible coordinate for point z in the coordinate plane on the left is (1.2, 8.7). In the graph in the middle, notice that each tick mark on the x-axis is 1 unit, but each tick mark on the y-axis is two units; also, z has a negative x value because it is to the left of the y-axis. A valid coordinate of point z for the middle coordinate plane is therefore (-2.4, 6.4). Finally, on the graph on the right, notice that each tick mark on the x-axis is 0.5 units, while each tick mark on the y-axis is 2 units; therefore, a plausible coordinate value for point z is (0.8, -5.1).

• Distance between points Coordinate distance questions, too, are relatively straight forward, especially if you notice that the coordinate plane is really a grid. You can either count the grid marks to determine distance or you can use the distance formula, which itself is derived from the Pythagorean’s theorem.

  

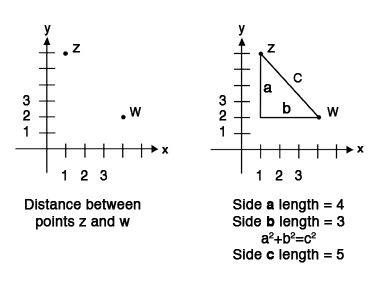
  Looking at the graph on the left, you are asked to find the distance between points z and w. Because the coordinate plane is really a grid, you can form a right triangle, denoted by sides a, b, and c on the right coordinate plane, from this you can use the Pythagorean’s theorem to determine the length of the hypotenuse, which is the distance between the two points.