Review
GRE Geometry - Educated Elimination
One of the most successful (and easier) methods to employ when you are stumped on a geometry problem (or any math question, for that matter), is to look at the various answers and see which of them is or are not possible. If you can eliminate at least one of the possible answer choices, then your chance of guessing correctly is dramatically increased. Consider the simple example:
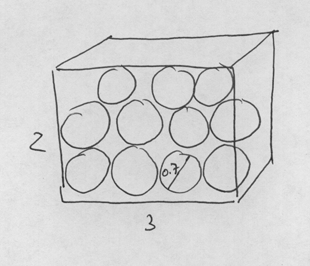
If a box three feet wide, 2 feet tall, and 1 foot in depth is filled with balls that are 0.7 feet in diameter, then which of the following values is a likely indicator of the maximum number of balls that can fit into the box?.
a. 03
b. 07
c. 11
d. 15
e. 24
Okay, we admit that this is a complicated problem, and it would take some time to figure out because you are not told beforehand exactly how the balls can be aligned. Regardless, you are told that the narrowest dimension of the box is 1 foot, and the balls are 0.7 feet in diameter, so at most one ball can fit across the narrowest dimension, and at most two balls can fit along the next smallest dimension, which is 2 feet. So if the question were asking how many circles of diameter 0.7 can fit inside a box that is 1 by 2 feet, then the answer would be 2. The last dimension, 3 feet, divided by 0.7 feet is approximately 4, so four balls can fit within the largest dimension if the balls are aligned along a straight line. The rest takes some tricky calculations, but already you can eliminate choice a and b, because we know that at least 8 balls can fit into the box.
Can 15 balls fit into the box? Two balls (which fit into the two smallest dimensions), times approximately 4 balls (which fit into the largest dimension), equals 8, so even if the balls were aligned in a crisscross pattern, chances are that 15 balls could not fit; which leaves only c, 11 balls. The important thing to notice here is that no lengthy calculations were required, but instead you can arrive at the answer (or at least eliminate impossible choices) by thinking through the problem. Here is what you may have drawn on your scratch paper as you worked through the problem: