A polygon is a closed figure composed of line segments that meet at endpoints. We've already seen triangles, squares, parallelograms, and rectangles, and all of these are polygons, but there are non-regular polygons that you should be aware of. For example, here are several polygons that are not a triangle, a square, a parallelogram, or a rectangle:

Notice that all of these shapes are closed, and lines intersect only at their ends.

So why are polygons important? For several reasons, the most important of which is that polygons appear on some of the more challenging problems on the GRE. Luckily, with a little bit of practice, you should be able to manipulate polygons as easily as you can manipulate squares, triangles, rectangles, etc.

First, notice that there are several special polygons (aside from a triangle, square, rectangle), etc., that are given special names. These names are related to the number of sides and angles in the polygon. The term "gon" means shape, and if preceded by a numerical identifier, then the combined word describes the polygon. For example, "hexa" means 6, and "penta" means 5, so a hexagon has 6 sides and a pentagon has 5 sides. In addition, a regular polygon is one where all of the sides are equal in length. To designate that sides are equal in length, we either indicate that by writing the length of the side or by drawing hatch marks indicating equal lengths. Here are several examples of polygons, both regular and non-regular. Notice that a square is also a polygon -- all squares are also polygons, but not all polygons are squares. Don't let the terminology fool you.

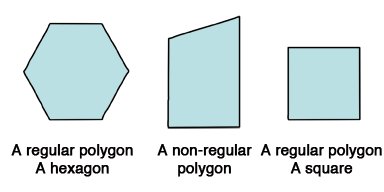
So what's the big deal about all these polygons? Well, there really isn't one. Once you have the basics down, the GRE geometry questions involving polygons should be straight-forward. Most importantly, you should understand that complex polygons can be divided into smaller polygons, which then makes the computation of area and perimeter much easier.

For example, assume you are asked to calculate the area of the polygon on the left. There is no straight-forward formula, but if you divide the polygon into smaller, easier polygons, you'll see that you can easily perform the area calculation. The polygon can be sectioned into two triangles and a rectangle, after which it is easy to then calculate the total area:

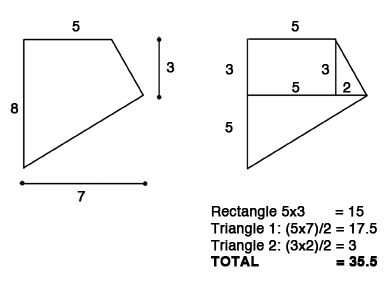
The above question is precisely the type of GRE question that you can expect -- questions that rely on only the most basic math concepts, but which require you to use those concepts in a creative fashion.

A parallelogram is a four-sided figure, just like a rectangle or a square. However, unlike a square, all sides do not have to be of equal length, and unlike a square or a rectangle, the angles that are formed by the sides of the parallelogram do not have to be 90 degrees. Here are a few examples of parallelograms:

The only facts that you have to remember about parallelograms is that the area is the same as a rectangle, base times height, and that in order for a shape to be a parallelogram, opposite sides must be of equal length and angles opposite of each other are the same measure.