Pythagorean's Theorem exploits very important characteristics of a right triangle. You should be familiar with the Pythagorean's Theorem because it will allow you answer quickly GRE geometry questions that ask you about the lengths of the sides of a right triangle. Visually, given a right triangle, with sides x, y, and z:

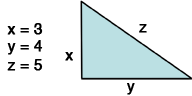
Note that z is the hypotenuse of the triangle, and x and y are the legs of the right triangle.

If you "plug in" the values for x, y and z into the equation, you get 3²+4²=5², which simplifies to 9+16=25. Sounds simple enough, right? Good. Because it is.

So how can you use this relationship, or how might a geometry question on the GRE exam require you to apply Pythagorean's Theorem? Assume that you were given the above triangle, except that you were given only the values for x and z, and instead you were asked to calculate the value of y. This is how you would go about answering such a question:

1. Write out the original question: x²+y²=z²
2. "Plug in" the know values: 3 ²+y²=5²
3. Simplify as much as you can: 9+ y²=25
4. Subtract 9 from both sides of the equation: y²=16

At which point, the question has been changed so that it asks you to determine, "what value squared yields 16?" The answer is, 4.