A square is a special kind of rectangle, in that all of the sides are equal in length, not just opposite sides. The area of a square is base times height, but because all sides are equal, we usually say that the area of a square is length of a side squared. The perimeter of a square is four times the length of one of the sides. Example squares, with their area and perimeter indicated:

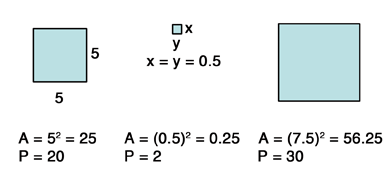
Notice that a square can be designated in one of several ways. All sides can be labeled, the sides can be given variables, such as x and y, the shape can be indicated to be a square, etc. As long as you know that a shape is a square, all that you need to know is the length of one side, after which it is then easy to determine the area and perimeter.

A few of the trickier GRE math problems will require you to calculate or use diagonals. A diagonal is just what it sounds, it diagonally connects two opposite corners of a square (a rectangle can have a diagonal, too). In the case of a square, we use the Pythagorean Theorem to derive the relationship between a side of a square and the diagonal of a square.

A rectangle is a four-side figure where opposite sides are equal in length and the four angles are all right angles. The are formula for a rectangle is simply base times height, while the perimeter of a rectangle, or the total distance of its sides, is 2 times the length plus 2 times the width. Rectangles are fairly straight forward, and you should definitely know the area and perimeter formulas by heart. Examples of rectangles, their areas, and perimeters, where A = Area and P = Perimeter:

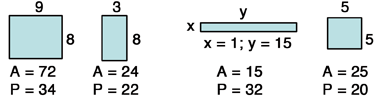
Notice the following facts:

• In the third rectangle, the height is x and width is y, and the values for x and y are given, so simple substitution gives the desired area and perimeter values.
• There is no relationship between the height and width of a rectangle. For example, in the first rectangle, the area is much greater than the perimeter, while in the third rectangle, the perimeter is much greater than the area.
• A square, the fourth figure, is also a rectangle in which the height and width are equal.